RSA加密算法

注: 下文中的 % 符号一律表示取模(mod)操作,而非取余(rem).

取模(Python)

1 2	8 % -5 = -2 -8 % 5 = 2

取余(JavaScript)

1 2	8 % -5 = 3 -8 % 5 = -3

RSA 算法

1 随机选择两个不同的质数 p 和 q.

2 计算 p * q, 记为 n.

3 计算卡迈尔克函数 λ(n).
因为 n = pq, 且 p 和 q 均为质数, 则 λ(n) 为 φ(p) 和 φ(q) 的最小公倍数.
$λ(n) = lcm(λ(p), λ(q)) = lcm(φ(p), φ(q)) = lcm(p -1 , q - 1) = \frac{/(p - 1)(q - 1)/}{gcd(p - 1, q - 1)}$

4 随机选择一个整数 e, 满足 1 < e < λ(n) , 并且 e 和 λ(n) 互质.通常会选择 65537 作为 e 的值.

5 计算 e 的模反元素 d, 即 $de \equiv 1 \ (mod \ λ(n))$ .

6 将 n 和 e 作为公钥, n 和 d 作为私钥.

加密: $c(m) = m^e \ mod \ n$

解密: $m = c^d \ mod \ n$

注意: m 必须满足 | m | < n

维基百科 RSA

代码实现:

// 计算最大公约数
function gcd(a, b) {
  if ((a, b)) {
    [a, b] = [b, a];
  }
  while (b > 0) {
    [a, b] = [b, a % b];
  }
  return a;
}
// 计算最小公倍数
function lcm(a, b) {
  return Math.abs(a * b) / gcd(a, b);
}
// 计算贝祖等式 的 x, y 值及 最大公约数
function extEuclid(a, b) {
  let [s0, s1] = [1, 0];
  let [t0, t1] = [0, 1];
  while (b > 0) {
    let q = Math.floor(a / b);
    [a, b] = [b, a - q * b];
    [s0, s1] = [s1, s0 - q * s1];
    [t0, t1] = [t1, t0 - q * t1];
  }
  return {
    x: s0,
    y: t0,
    gcd: a,
  };
}
// 模
function mod(a, b) {
  return ((a % b) + b) % b;
}
// 计算 e 和模λn 的模反元素 d
// de ≡ 1 (mod λn)
function modInv(e, λn) {
  // ed + λny = 1
  let d = extEuclid(e, λn).x;
  while (d < 0) {
    d += λn;
  }
  return d;
}

// 加密
function encrypt(m, publicKey) {
  const n = BigInt(publicKey.n);
  const e = BigInt(publicKey.e);
  return mod(BigInt(m) ** e, n);
}

// 解密
function decryption(c, privateKey) {
  const n = BigInt(privateKey.n);
  const d = BigInt(privateKey.d);
  return mod(BigInt(c) ** d, n);
}

const p = 61;
const q = 53;
const e = 17;
n = p * q; // 3233

λn = lcm(p - 1, q - 1); // 780
d = modInv(e, λn); // 413
// φn = (p - 1) * (q - 1) // 3210
// d = modInv(e, φn); // 2753

const publicKey = { n, e };
const privateKey = { n, d };

const c = encrypt(65, publicKey);
console.log(c); // 2790
const m = decryption(c, privateKey);
console.log(m); // 65

注意: JavaScript 的 % 符号表示取余(rem)运算, 不是取模(mod).

卡迈尔克函数(λ)也可以替换成欧拉函数(φ),同样满足要求.

// λn = lcm(p - 1, q - 1); // 780
//d = modInv(e, λn); // 413

φn = (p - 1) * (q - 1); // 3210
d = modInv(e, φn); // 2753

另外, λn 和 φn 的任意倍数也能使算法成立.

1
2
3

λn = lcm(p - 1, q - 1) * 100;
//or
φn = (p - 1) * (q - 1) * 100;

在实际应用中,会使用 CRT 定理, 加快计算速度.

// 计算最大公约数
function gcd(a, b) {
  if ((a, b)) {
    [a, b] = [b, a];
  }
  while (b > 0) {
    [a, b] = [b, a % b];
  }
  return a;
}
// 计算最小公倍数
function lcm(a, b) {
  return Math.abs(a * b) / gcd(a, b);
}
// 计算贝祖等式 的 x, y 值及 最大公约数
function extEuclid(a, b) {
  let [s0, s1] = [1, 0];
  let [t0, t1] = [0, 1];
  while (b > 0) {
    let q = Math.floor(a / b);
    [a, b] = [b, a - q * b];
    [s0, s1] = [s1, s0 - q * s1];
    [t0, t1] = [t1, t0 - q * t1];
  }
  return {
    x: s0,
    y: t0,
    gcd: a,
  };
}
// 模
function mod(a, b) {
  return ((a % b) + b) % b;
}
// 计算 e 和模λn 的模反元素 d
// de ≡ 1 (mod λn)
function modInv(e, λn) {
  // ed + λny = 1
  let d = extEuclid(e, λn).x;
  while (d < 0) {
    d += λn;
  }
  return d;
}

// 加密
function encrypt(m, publicKey) {
  const n = BigInt(publicKey.n);
  const e = BigInt(publicKey.e);
  return mod(BigInt(m) ** e, n);
}

// 解密
function decryption(c, privateKey) {
  const dP = BigInt(privateKey.dP);
  const dQ = BigInt(privateKey.dQ);
  const qInv = BigInt(privateKey.qInv);
  const p = BigInt(privateKey.p);
  const q = BigInt(privateKey.q);
  c = BigInt(c);
  const m1 = mod(c ** dP, p);
  const m2 = mod(c ** dQ, q);
  let h = mod(qInv * (m1 - m2), p);
  return m2 + h * q;
}

const p = 61;
const q = 53;
const e = 17;
n = p * q; // 3233

λn = lcm(p - 1, q - 1); // 780
d = modInv(e, λn); // 413
// φn = (p - 1) * (q - 1) // 3210
// d = modInv(e, φn); // 2753

dP = mod(d, p - 1); // 53
dQ = mod(d, q - 1); // 49
qInv = modInv(q, p); // 38
const publicKey = { n, e };
const privateKey = { n, d, dP, dQ, qInv, p, q };

const c = encrypt(65, publicKey);
console.log(c);
const m = decryption(c, privateKey);
console.log(m);

同余

当两个整数除以同一个正整数，若得相同余数，则二整数同余。
两个整数 a，b，若它们除以正整数 m 所得的余数相等，则称 a，b 对于模 m 同余
记作 $a \equiv b \ (mod \ m)$
读作 a 同余于 b 模 m，或读作 a 与 b 关于模 m 同余。

维基百科同余

例如
$26 \equiv 14 \ (mod \ 12)$
即 26 和 14 关于模 12 同余, 26 % 12 = 14 % 12

$-8 \equiv 7 \ (mod \ 5)$
即 -8 和 7 关于模 5 同余, -8 % 5 = 7 % 5

当 $a \equiv 1 \ (mod \ n)$ 时, 即
例如 $81 \equiv 1 \ (mod \ 5)$ , 81 % 5 = 1 % 5 = 1

费马小定理

假如 a 是一个整数，p 是一个质数，那么 $a^{p}-a$ 是 p 的倍数，可以表示为
$a^p \equiv a \ (mod \ p)$

维基百科费马小定理

例如
$4^{3} \equiv 4 \ (mod \ 3)$
64 % 3 = 4 % 3 = 1

如果 a 不是 p 的倍数, 这个定理也可以写成
$a^{p-1} \equiv 1 \ (mod \ p)$

即如果 p 是质数, 且 a 不是 p 的倍数时, $a^{p-1}$ % p = 1.
例如:
$2^{5 - 1} \equiv 1 \ (mod \ 5)$
16 % 5 = 1

$2^{100} \equiv 1 \ (mod \ 101)$
(2 ** 100) % 101 = 1

欧拉定理(φ 函数定理)

若 n,a 为正整数，且 n,a 互质（即 gcd(a,n)=1, a 和 n 的最大公约数为 1），则
$a^{φ(n)} \equiv 1 \ (mod \ n)$
即 $a^{φ(n)}$ 与 1 在模 n 下同余；φ(n) 为欧拉函数
欧拉定理实际上是费马小定理的推广

维基百科欧拉定理

例如 a = 3, n = 5

$3^{φ(5)} \equiv 1 \ (mod \ 5)$
$3^{4} \equiv 1 \ (mod \ 5)$
81 % 5 = 1

欧拉函数

对正整数 n，欧拉函数 φ(n) 是小于或等于 n 的正整数中与 n 互质的数的数目

维基百科欧拉函数
即计算在 1 ~ n 中,有多少个数和 n 为互质关系

计算方式如下:
1 如果 n = 1, 则 $φ(1) = 1$ . (1 和任何数互质, 包括自身在内)

2 如果 n 为质数 p 的 k 次幂(n = $p^k$ ), 则 $φ(n) = φ(p^k) = p^k - p^{k - 1} = (p - 1)p^{k - 1}$
例如 $φ(9) = 3^2 - 3 = 6$

3 如果 n = pq, 且 p 和 q 互质, 则 $φ(n) = φ(pq) = φ(p) φ(q)$
例如 $φ(72) = φ(8 * 9) = φ(8) φ(9) = (2^3 - 2^2) * (3^2 - 3) = 24$

4 如果 n 为质数, 则 $φ(n) = n - 1$
例如 $φ(5) = 5 - 1 = 4$ ( 5 和 1, 2, 3, 4 互质)
根据欧拉定理, 如果 n 为质数, 且 a 与 n 互质,则 $a^{φ(p)} = a^{p - 1} \equiv 1 \ (mod \ p)$
例如:
$5^{φ(4)} = 5^{4 - 1} \equiv 1 \ (mod \ 4)$
125 % 4 = 1

卡迈尔克函数

当 n 为 1, 2, 4, 奇质数的次幂, 奇质数的次幂的两倍时
λ(n) = φ(n)
当 n 为 2 的次幂时(不包括 2, 4 )
$λ(n) = \frac{1}{2} φ(n)$

正整数 n 可以分解为任意质数相乘, λ(n) 为这些质数的 λ 值的最小公倍数

$n = p_{1}^{r_1}p_2^{r_2} \dots p_k^{r_k}$
$λ(n) = lcm(λ(p_{1}^{r_1}), λ(p_{2}^{r_2}) \dots, λ(p_k^{r_k}) )$

欧几里德算法(辗转相除法)

辗转相除法用于计算两个整数的最大公约数 , 其原理为: 两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数

维基百科辗转相除法

例如计算 252 和 105 的最大公约数
252 % 105 = 42
105 % 42 = 21
42 % 21 = 0

因此 252 和 105 的最大公约数为 21

代码实现

function gcd(a, b) {
  if ((a, b)) {
    [a, b] = [b, a];
  }
  while (b > 0) {
    [a, b] = [b, a % b];
  }
  return a;
}
console.log(gcd(252, 105));

扩展欧几里德算法

扩展欧几里得算法（英语：Extended Euclidean algorithm）是欧几里得算法的扩展。
已知整数 a、b，扩展欧几里得算法可以在求得 a、b 的最大公约数的同时，能找到整数 x、y（其中一个很可能是负数），使它们满足贝祖等式
ax + by = gcd(a, b)
如果 a 是负数，可以把问题转化成
|a|(-x) + by = gcd(|a|, b)

维基百科扩展欧几里德算法

例如 a = 240 b= 46
240x + 46y = gcd(240, 46) = 2
解得 x = -9, y = 47 满足 ax + by = gcd(a, b)
240* (-9) + 46 * 47 = 2

代码实现

function extEuclid(a, b) {
  let [s0, s1] = [1, 0];
  let [t0, t1] = [0, 1];
  while (b > 0) {
    let q = Math.floor(a / b);
    [a, b] = [b, a - q * b];
    [s0, s1] = [s1, s0 - q * s1];
    [t0, t1] = [t1, t0 - q * t1];
  }
  return {
    x: s0,
    y: t0,
    gcd: a,
  };
}
console.log(extEuclid(240, 46));

假如两个正整数 a b 互质, 则有 ax + by = 1
(如果两个正整数互质, 则他们的最大公约数为 1)

最大公约数

greatest common divisor, 简称 gcd

维基百科最大公约数

代码实现

function gcd(a, b) {
  if ((a, b)) {
    [a, b] = [b, a];
  }
  while (b > 0) {
    [a, b] = [b, a % b];
  }
  return a;
}

最小公倍数

least common multiple, 简称 lcm

维基百科最小公倍数

最小公倍数和最大公约数间的关系如下

$lcm(a, b) = \frac{|a b|}{gcd(a, b)}$

代码实现

function gcd(a, b) {
  if ((a, b)) {
    [a, b] = [b, a];
  }
  while (b > 0) {
    [a, b] = [b, a % b];
  }
  return a;
}
function lcm(a, b) {
  return Math.abs(a * b) / gcd(a, b);
}

模反元素

如果正整数 a 和 m 互质, 一定能找到一个整数 x, 使 ab 满足如下等式:
$ax \equiv 1 \ (mod \ m)$
ab % m = 1, 即 ab - 1 可以被 m 整除
整数 x 即为正整数 a 的模反元素

维基百科模反元素

可通过扩展欧几里德算法可以算出模反元素 x
模反元素不只有一个, $x + km ( k \in Z )$ 都是 a 关于 m 的模反元素

因为互质正整数的最大公约数为 1
ax +my = gcd(a, m) = 1
两侧互换, 可以发现 ax - 1 等于 -y 倍的 m, 即 ax 除以 m 的余数为 1
ax - 1 = (-y)m
符合 $ax \equiv 1 \ (mod \ m)$

代码实现

function extEuclid(a, b) {
  let [s0, s1] = [1, 0];
  let [t0, t1] = [0, 1];
  while (b > 0) {
    let q = Math.floor(a / b);
    [a, b] = [b, a - q * b];
    [s0, s1] = [s1, s0 - q * s1];
    [t0, t1] = [t1, t0 - q * t1];
  }
  return {
    x: s0,
    y: t0,
    gcd: a,
  };
}
function modInv(a, m) {
  const bezout = extEuclid(a, m);
  let d = bezout.x;
  if (bezout.gcd !== 1) {
    throw new Error("No Modular multiplicative inverse");
  }
  // 得到的 d 可能是负的, 一般取最小的正整数
  // d 加上任意个 m 还是 a 关于 m 的模反元素
  while (d < 0) {
    d += m;
  }
  return d;
}

console.log(modInv(2, 3)); // 2
console.log(modInv(2, 4)); // Error: No Modular multiplicative inverse

使用 Node 生成 rsa 密钥

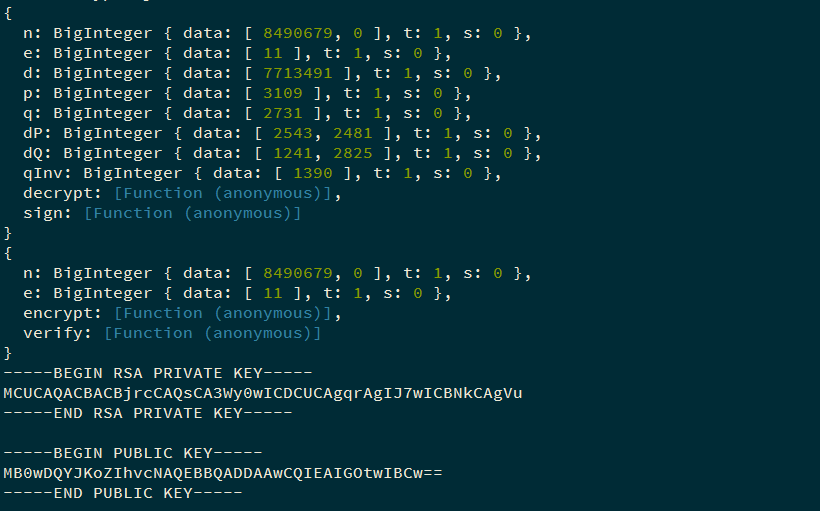
可用 node-forge 的 pki.rsa.generateKeyPair 方法来生成一组密钥对.
pki.rsa.generateKeyPair 用于生成一组密钥对, 其中包含一个公钥和一个私钥.
参数 1 为密钥 n 二进制格式的长度,默认为 2048.
参数 2 接受一个质数作为参数,用于指定密钥 e 的值, 默认为 65537 (二进制 0x10001).

node-forge 在内部调用 Node 自带模块 crypto 来生成密钥对.
然后调用 pki.privateKeyFromPem 和 pki.publicKeyFromPem 将密钥转成易读的格式.

const forge = require("node-forge");
const pki = forge.pki;

const keys = pki.rsa.generateKeyPair(24, 11);
console.log(keys.privateKey);
console.log(keys.publicKey);
console.log(pki.privateKeyToPem(keys.privateKey));
console.log(pki.publicKeyToPem(keys.publicKey));

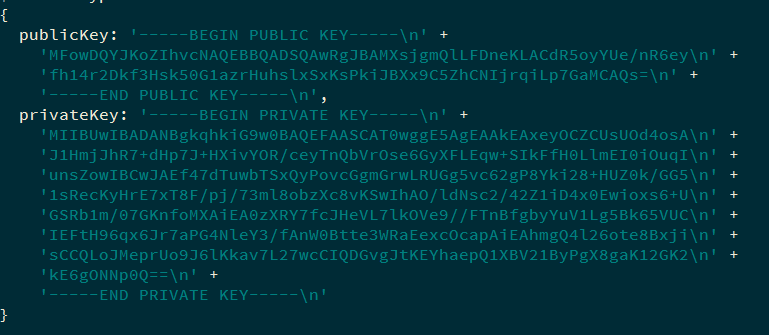
const crypto = require("crypto");
const keys = crypto.generateKeyPairSync("rsa", {
  modulusLength: 512, // 长度
  publicExponent: 11, // e 值
  publicKeyEncoding: {
    type: "spki",
    format: "pem",
  },
  privateKeyEncoding: {
    type: "pkcs8",
    format: "pem",
  },
});
console.log(keys);

参考

RSA 算法原理（一） - 阮一峰的网络日志
 encryption - Euler's totient function and Carmichael's totient function in RSA - Cryptography Stack Exchange
RSAES-OAEP Encryption Scheme