84 Largest Rectangle in Histogram

题目

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

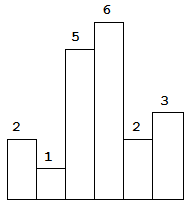
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

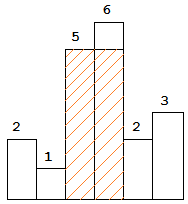
The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

1 2	Input: [2,1,5,6,2,3] Output: 10

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

解题思路

求解可表示的最大矩形面积,需要知道每个整数(heights[i])可表示的最大面积.
可以依次遍历 heights 中元素, 找出 heights[i] 左右两侧第一个比 heights[i] 小的元素.即可算出 heights[i] 的最大可覆盖面积.
以 [1, 3, 4, 5, 2, 6, 1] 中的 2 为例.
在 2 的左右两侧, 比 2 小的整数的下标为 0 和 6.则 2 的最大可覆盖面积为:

(right - left - 1) * height = (6 - 0 - 1) * 2= 8

0 1 2 3 4 5 6 (下标)
-------------
1 3 4 5 2 6 1

left  = 0
right = 6

如果在遍历 heights 时, 每次都向两侧查找 heights[i] 的边界,则其时间复杂度为 $O(n^2)$ .
(遍历一遍 heights 为 n, 每个 heights[i] 还需要分别往左右两侧各跑一次合计为 n.)

可以利用单调栈的性质,快速定位 heights[i] 的左右边界,将其时间复杂度降为 $O(n)$ .
(只需要跑一趟)

单调栈可以分为单调递增栈和单调递减栈两种,其栈内元素从栈尾到栈顶依次递增(单调递增栈, 栈顶元素最大,栈尾元素最小)/依次递减(单调递减栈, 栈顶元素最小, 栈尾元素最大).

创建一个单调递增栈 stack = [-1] 来储存 heights[i] 的下标 i. 其中的 -1 作为守卫,代表 heights[0] 的 left, 避免操作数组时越界.

以 [3, 3, 4, 5, 2, 6, 1] 中的 2 为例.
在 2 的左侧, 没有比 2 小的元素,因此去 -1 作为左侧的边界.2 的最大可覆盖面积为:

(6 - (-1) - 1) * 2 = 12

-1 0 1 2 3 4 5 6 (下标)
-----------------
   3 3 4 5 2 6 1

left  = -1
right = 6

然后依次遍历 heights 中元素.
如果 heights[i] 大于/等于 heights[stack[top]],则将 heights[i] 推入栈中.
如果 height[i] 小于 heights[stack[top]],则先计算 heights[stack[top]] 可表示的最大面积,因为:

i 一定是 stack[top] 的 right(右边界, stack[top] 右侧的第一个比 stack[top] 小的值).
stack[top - 1] 一定是 stack[top] 的 left(左边界, 比 heights[stack[top]] 大的都被弹出去了).

以 [2, 3, 1] 中的 3 为例:

0 1 2 (下标)
-----
2 3 1

left  = 0
right = 2

当遍历到 1 时, stack = [1, 0, -1]
因为 2 3 比 1 大, 所以 1 一定是 2 3 的 right(右边界).
此时 3 左边界为 heights[stack[top - 1]] = 0, 其最大面积为:

1	(2 - 0 - 1) * 3 = 3

然后将 heights[stack[top]] 从栈中弹出,将 height[i] 推入栈中.
遍历结束后, 如果 stack.length > 1 (栈里还有除守卫(-1)外的其他下标),则此时的 right 一定是 heights.length.

例如 [1, 2, 3]. 因为其本身就是递增关系, 所以不会触发出栈操作.当 heights 遍历结束时, 其 stack 为:

1	stack = [2, 1, 0, -1];

此时 heights 元素 1, 2, 3 的 left (左边界) 下标分别为 -1, 0, 1, right (右边界) 为最后一个元素的右侧.

0 1 2 3 (下标)
----------------
1 2 3

right = 3

使用 JavaScript 的数组模拟栈的操作:

stack[0] 为获取栈顶元素
stack[1] 为栈顶的下一个元素
stack[stack.length - 1] 为获取栈底元素
stack.unshift() 入栈
stack.shift() 出栈(获取值并将其从栈顶删除)

function largestRectangleArea(heights) {
  // 用数组模拟栈
  const stack = [-1];
  let maxArea = 0;
  for (let i = 0; i < heights.length; i++) {
    // 因为 heights[i] < heights[stack[0]], 所以 i 一定是 stack[0] (栈顶元素)的右边界.
    while (stack[0] > -1 && heights[i] < heights[stack[0]]) {
      const height = heights[stack[0]];
      // 计算栈顶元素的最大可面积, 与之前的最大面积比较
      maxArea = Math.max(maxArea, height * (i - stack[1] - 1));
      // 出栈
      stack.shift();
    }
    // 入栈
    stack.unshift(i);
  }
  // 栈中除了 -1 外还有别的下标
  while (stack[0] > -1) {
    const height = heights[stack[0]];
    // 判断剩余元素可表示的最大面积
    maxArea = Math.max(maxArea, height * (heights.length - stack[1] - 1));
    stack.shift();
  }
  return maxArea;
}